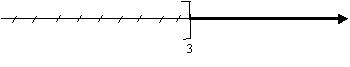3^ème

COLLÈGE NAZARETH

BREVET BLANC N°2-2005-

MATHÉMATIQUES

Durée : 2 heures.

Les calculatrices sont autorisées ainsi que les instruments usuels de dessin.

Présentation, orthographe et rédaction : 4 points.

L’annexe est à rendre avec votre copie.

Partie I : Activités numériques (12 points)

EXERCICE 1 : ( /3)

1. Soit : A = –  : .
Calculer A en détaillant les étapes du calcul et écrire le résultat sous la forme d’une fraction irréductible.
2. Soit B = ^².
Écrire B sous la forme a + b , où a, b et c sont des nombres entiers (On indiquera les étapes des calculs).
3. Soit C = – 7 + .
Écrire C sous la forme a où a et b sont des nombres entiers.

EXERCICE 2 : ( /3,5)

On pose : D = 4² – 25 – (2+ 5) (3– 7).
1. Développer et réduire D.
2. a) Factoriser 4² – 25.
b) En déduire une factorisation de D.

3. Résoudre l’équation : (2+ 5) (2 –) = 0

EXERCICE 3 : (/1,5)

1. Résoudre l’inéquation : 5 – 2 < – 4.

2. Représenter l’ensemble des solutions sur une droite graduée.

EXERCICE 4 : (/2,5)

Un commerçant augmente les prix de tous ses articles de 8%.

Un objet coûte x euros. Après avoir subi cette augmentation, il coûte y euros.

1. Exprimer y en fonction de x.

2. Un lecteur de DVD coûte, avant augmentation, 329 euros. Combien coûtera-t-il après ?

3. Un téléviseur coûte, après augmentation, 540 euros. Combien coûtait-il avant ?

EXERCICE 5 : (/1,5)
Le 7 Novembre 1998, au retour du second voyage historique de John Glenn dans l’Espace, la navette spatiale Discovery avait parcouru 5,8 millions de kilomètres.
Cette mission ayant duré 8 jours et 22 heures, calculer la vitesse moyenne en km/h de la navette.
On donnera le résultat en écriture décimale arrondie au km/h, puis en écriture scientifique.

1/3

Partie II : Activités géométriques (12 points)

EXERCICE 1 : ( /3,5)

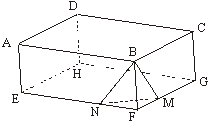ABCDEFGH est un parallélépipède rectangle.

On donne :

FE = 12 cm ; FG = 9 cm ; FB = 3 cm ;

FN = 4 cm ; FM = 3 cm.

1. Calculer la longueur MN.

2. Montrer que l’aire du triangle FNM est égal à 6 cm².

3. Calculer le volume de la pyramide (P) de sommet B et de base le triangle FNM.

4. On considère le solide ABCDENMGH obtenu en enlevant la pyramide (P) au parallélépipède rectangle.
a. Quel est le nombre de faces de ce solide ?
b. Calculer son volume.

EXERCICE 2 : ( /5,5)

L’unité de longueur est le centimètre.

RST est un triangle tel que RS = 6,4 ST = 8 et RT= 4,8

1. Construire la figure en vraie grandeur sur l’annexe 1 (que vous compléterez au fur et à mesure).

2. Démontrer que le triangle RST est rectangle en R.

3. Calculer la valeur arrondie au degré près de la mesure de l’angle .

4. M est le point du segment [SR] tel que SM = 4 et N est le point du segment [ST] tel que SN = 5.

a. Démontrer que les droites (MN) et (RT) sont parallèles.

b. Calculer la distance MN.

EXERCICE 3 : ( /3)

Pour cet exercice, utiliser la feuille annexe.

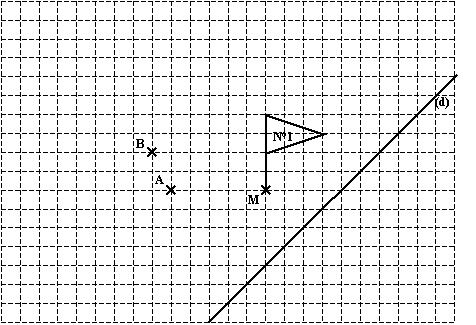
Sur un quadrillage constitué de carrés, on a placé une droite (d), trois points (nommés A, B et M), une figure qui est en forme de fanion et est numérotée 1 (voir annexe).

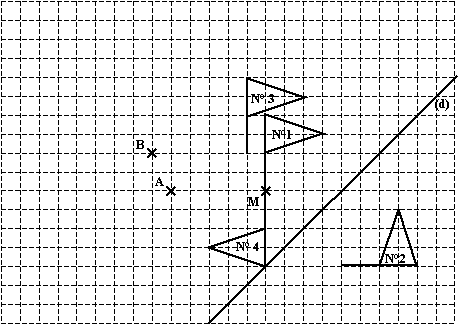
a. Construire l'image de la figure 1 par la symétrie d'axe (d) ; numéroter 2 la figure obtenue.

b. Construire l'image de la figure 1 par la translation de vecteur ; numéroter 3 la figure obtenue.

c. Construire l'image de la figure 1 par la symétrie de centre M ; numéroter 4 la figure obtenue.

2/3

Partie III : Problème (12 points)

Un fournisseur d’accès à Internet propose à ses clients 2 formules d’abonnement :

• Une formule A comportant un abonnement fixe de 20 € par mois auquel s’ajoute le prix des communications au tarif préférentiel de 2 € de l’heure.
  
  
• Une formule B offrant un libre accès à Internet mais pour laquelle le prix des communications est de 4 € pour une heure de connexion.

Dans les deux cas, les communications sont facturées proportionnellement au temps de connexion.

1. Pierre se connecte 7 h 30 min par mois et Annie 15 h par mois.
   · Calculer le prix payé par chacune des deux personnes selon qu’elle choisit la formule A ou la formule B.
   · Conseiller à chacune l’option qui est pour elle la plus avantageuse.
   
   
2. On note x le temps de connexion d’un client, exprimé en heures.

On appelle P_A le prix à payer en euros avec la formule A et P_B le prix à payer en euros avec la formule B.

Exprimer P_A et P_B en fonction de x.

3. Placer l’origine d’un repère orthogonal en bas et à gauche à l’aide du quadrillage fourni en annexe.
   En abscisses on choisit 1cm pour une unité et en ordonnées 1 cm pour 5 unités.
   Dans ce repère, tracer :

· la droite (d), représentation graphique de la fonction f  : x |¾® 2x + 20

· la droite (d’), représentation graphique de la fonction g : x |¾® 4x

4. En faisant apparaître sur le graphique précédent les traits nécessaires, répondre aux deux questions suivantes :

a) Coralie, qui avait choisi la formule B a payé 26 €. Combien de temps a-t-elle été connectée ?

b) Jean se connecte 14 h dans le mois. Combien va-t-il payer selon qu’il choisit la formule A ou la formule B ?

5. a) Résoudre l’équation : 4x = 2x + 20.
b) Que permet de déterminer la résolution de cette équation dans le contexte du problème ?

3/3

Annexe à rendre avec la copie

NOM :
………………………………………

Partie II/ Exercice 3 :

Partie III / Problème- Question 3.

3^ème A - B	BB2-2005 MATHÉmatiques	Coefficient : 4 Note sur : 40 Présentation : /4
Date : 02/05/2005 Durée : 2h	Correction

Partie I : Activités numériques (12 points)

EXERCICE 1 : ( /3)

A = A = A = A = A = A =

B = ^² B = 3 – 2 + 2 B = 5 – 2

C = – 7 + C = – 7 + C = – 710 + 2 C = (1 – 70+2) C = – 67

EXERCICE 2 : ( /3,5)

1.Développer D : D = 4² – 25 – (2+ 5) (3– 7). D = 4² – 25 – (6² – 14 +15 – 35) D = 4² – 25 – 6² + 14 – 15 + 35 E = –2² – + 10

2.Factoriser . a) 4² – 25 = (2)² – 5² a² – b² 4² – 25 = ( 2 – 5) (2 +5) b) D = (2 – 5) (2 +5) – (2+ 5) (3– 7) D = (2 +5) [(2 – 5) – (3– 7)] D = (2 +5) (2 – 5 – 3 + 7) D = (2 + 5) (2 – )

3.l’équation (2 + 5) (2 – ) = 0 est de la forme AB=0, ce qui revient à résoudre A=0 ou B=0, soit :
2 + 5 = 0 ou 2 – = 0
2= – 5 ou –= – 2
= – ou = 2 L’équation admet deux solutions – et 2

EXERCICE 3 : (/1,5)

1. 5 – 2 < – 4 soit : – 2 – < – 4 – 5 – 3 < – 9 > > 3

2. L’ensemble des solutions est représenté par la partie non hachurée.

EXERCICE 4 : (/2,5)

1. y= (1 + 0,08) x y = 1,08x

2. Ici x = 329 ; d’après 1. y = 1,08 329 = 355,32

Le lecteur DVD coûtera 355,32 euros.

3. Ici y = 540. D’après 1., si 540 = 1,08x et alors x = x = 500 Le téléviseur coûtait 500 euros.

EXERCICE 5 : (/1,5)

d = 5,8 millions de km = 5 800 000 km ; t = 8jours+ 22 heures= 824 + 22 heures = 214 heures

Or v = soit v = v » 27 103 km/h

La vitesse de la navette est d’environ 27 103 km/h soit 2,7103 10⁴ km/h en écriture scientifique

1/3 correction

Partie II : Activités géométriques (12 points)

EXERCICE 1 : ( /3,5)

1. Dans le triangle MNF rectangle en F, on applique le théorème de Pythagore : MN² = FM² + FN² MN² = 3² + 4² MN² = 9 + 16 MN² = 25 d’où MN = MN = 5 cm.

2. Le triangle FNM est rectangle en F, son aire se calcule donc par : A = A = A = = 6 L’aire du triangle FNM est bien égale à 6 cm².

3. Calcul du volume de la pyramide (P) de sommet B et de base le triangle FNM.

La hauteur de cette pyramide est la longueur BF.

La formule du volume d’une pyramide nous donne : V = Aire(FNM) BF

D’où V = ´ 6 ´ 3 V= 6 .

La pyramide (P) de sommet B et de base le triangle FNM a donc un volume de 6 cm³.

3.a. Le solide ABCDENMGH obtenu en enlevant la pyramide (P) au parallélépipède rectangle possède 7 faces.

b. Son volume se calcule par différence du volume du parallélépipède rectangle ABCDEFGH et du volume de la pyramide (P).

Volume de ABCDEFGH : V₁ = FE ´ FG ´ FB V₁ = 12 ´ 9 ´ 3 V₁ =324 cm³

Volume du solide : V₁-V = 324 – 6 = 318.

Le solide ABCDENMGH a un volume de 318 cm³.

EXERCICE 2 : ( /5,5) 1. Figure

2. Calculons les carrés des mesures des côtés :

RS = 6,4 = 40,96

ST = 8 = 64

RT = 4,8 = 23,04 Or RS + RT = 40,96 + 23,04 = 64 donc ST = RS + RT

On en déduit, d’après la réciproque du théorème de Pythagore, que le triangle RST est rectangle en R.

3. Puisque le triangle RST est rectangle en R :

sin = = = 0,6 » 37° arrondi au degré près

4. a. D’une part = = 0,625 et d’autre part = = 0,625 donc =

De plus les points S, M et R sont alignés dans le même ordre que les points S, N et T donc d’après la réciproque du théorème de Thalès les droites (MN) et (RT) sont parallèles.

b. M est un point de (RS) et N est un point de (ST)
les droites (MN) et (RT) sont parallèles ; nous pouvons appliquer le théorème de Thalès :

= = soit = Ainsi MN = = 3 MN = 3 cm

EXERCICE 3 : ( /3)

	2/3 correction
2/3 correction

Problème :

1.

Calculons le prix payé par Pierre (7h30 de connections) : Formule A : 20 + 2 ´ 7,5 = 20 + 15 = 35 € Formule B : 4 ´ 7,5 = 30 €

Calculons ensuite le prix payé par Annie (15 h de connections) : Formule A : 20 + 2 ´ 15 = 20 + 30 = 50 € Formule B : 4 ´ 15 = 60 €

D’après ces résultats, Pierre a intérêt à choisir la formule B, tandis que Annie doit choisir la formule A.

2. Si P_A et P_B sont les prix à payer respectivement dans les formules A et B et le temps de connexion d’un client, exprimé en heures alors :
P_A = 2x + 20 P_B = 4x

3.Tracé des graphiques représentant les fonctions f et g : On peut utiliser les points calculés ci-dessus :

Pour représenter f : L’image de 0 est 20 ; l’image de 15 est 50 : (0 ;20) et (15 ;50)

Pour représenter g : L’image de 0 est 0 ; l’image de 15 est 60 : (0 ;0) et (15 ;60)

6h30

56

48

26

4. a. D’après le graphique précédent, on voit que si Coralie a payé 26 € avec la formule B, elle s’est donc connectée
6 h30 min.

b. De même, si Pierre se connecte 14 h, il paiera 48 € avec la formule A et 56 € avec la formule B.

5. Résolution de l’équation : 4 = 2x + 20.
4x – 2 = 20
2x = 20
x =

x = 10
Cette équation permet de déterminer le nombre d’heures de connections pour lequel le tarif B est équivalent au tarif A soit pour 10 heures de connexion.

3/3 correction