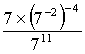COLLÈGE NAZARETH

BREVET BLANC N°1-2005-

MATHÉMATIQUES

Durée : 2 heures.

Les calculatrices sont autorisées ainsi que les instruments usuels de dessin.

Présentation, orthographe et rédaction : 4 points

Partie I : Activités numériques (12 points)

Exercice 1 : (/2,5)

Calculer les nombres A ; B et C. Écrire les étapes et donner les résultats sous forme de fractions irréductibles.
A = B = C=

Exercice 2 :(/3)

On considère l'expression : D = ( + 2)² – ( + 2) (5 – 1).

1. Développer et réduire D.

2. Factoriser D.

3. Résoudre l’équation ( + 2) ( – 4 + 3) = 0.

Exercice 3 :(/2,5)

Soit E = (7 – 3)² – 9.

1. Développer et réduire E.

2. Factoriser E.

3. Résoudre l’équation 7( 7 – 6) = 0.

Exercice 4 : (/1,5)

Rendre irréductible la fraction en détaillant les calculs.

Exercice 5 :(/2,5)

1. Calculer le PGCD des nombres 372 et 775. (on détaillera les calculs nécessaires).

2. Un chef d’orchestre fait répéter 372 choristes hommes et 775 choristes femmes pour un concert. Il veut faire des groupes de répétition de sorte que :
- le nombre de choristes femmes est le même dans chaque groupe.
- le nombre de choristes hommes est le même dans chaque groupe.
- chaque choriste appartient à un groupe.

a) Quel nombre maximal de groupes pourra-t-il faire ?
b) Combien y aura-t-il alors de choristes hommes et de choristes femmes dans chaque groupe ?

1/3

Partie II : Activités géométriques (12 points)

Exercice I :(/7)

L’unité de longueur est le centimètre.

RST est un triangle tel que : RS = 6,4 ; ST = 8 et RT = 4,8 .

1. Construire la figure en vraie grandeur.

2. Démontrer que le triangle RST est rectangle.

3. Calculer la valeur arrondie au degré près de la mesure de l’angle .
4. M est un point du segment [SR] tel que SM = 4,2
et N est un point du segment [ST] tel que SN = 5.
Les droites (MN) et (RT) sont-elles parallèles ? Justifier votre réponse.

Exercice II :(/5)

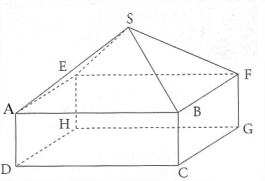
La maquette de la maison représentée ci-contre est composée : · d’un pavé droit de dimensions : AB = 30 cm, AE = 20 cm et AD = 5 cm · d’une pyramide SABFE de hauteur 6 cm. 1. Montrer que le volume V1 de cette maquette est égal à 4 200 cm^3.
2. Sachant que cette maquette est une réduction de coefficient 1/50 de la maison réelle, déduire de la première question le volume V2 en m^3 de la maison.

2/3

Partie III : Problème (12 points)

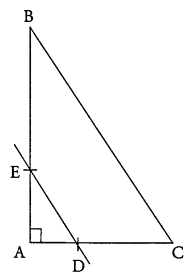
ABC est un triangle rectangle en A tel que AB = 9 cm et AC = 6 cm. D est le point du segment [AC] tel que AD = AC. E est le point du segment [AB] tel que la droite (DE) soit parallèle à la droite (BC). l. Reproduire la figure en grandeur réelle sur votre copie. 2. Calculer BC, puis en donner la valeur arrondie au centième. 3. Montrer par le calcul que AE = 3 cm. 4. Placer le point F sur le segment [AC] tel que AF = 4 cm. Placer le point G sur le segment [AB] tel que AG = 6 cm. Tracer le segment [FG]. 5. Démontrer que la droite (FG) est parallèle à la droite (BC).

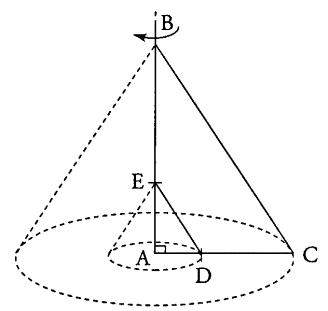
6. En tournant autour de la droite (AB) le triangle ABC engendre un cône C1. AB est sa hauteur et AC est le rayon de sa base. a) Calculer l'aire B1 de la base du cône en fonction de p. b) Calculer le volume V1 du cône C1 en fonction de p, puis donner la valeur du résultat arrondie au millième. 7. En tournant autour de la droite (AB) le triangle AED engendre un cône C2 de volume V2 : AE est la hauteur de ce cône, AD est le rayon de sa base. Le cône C2 est une réduction de C1 a) Quel est le coefficient de réduction ? b) Exprimer le volume V2 en fonction de V1.

BREVET BLANC N°1-2005-MATHÉMATIQUES- Correction

Partie I : Activités numériques (12 points)

Exercice 1 : (/2,5)

A = A = A = A = A = A =

B = B = B = B = B =

C= C = C = 7^1 + 8 – 11 C = 7^–2 C = C =

Exercice 2 :(/3)

On considère l'expression : D = ( + 2)² – ( + 2) (5 – 1).

1. Développer et réduire D. D = ( + 2)^2 – ( + 2) (5 – 1) D = ² + 4 + 4 – ( 5² – + 10 – 2) D = ² + 4 + 4 – 5² + – 10 + 2 D = – 4² – 5 + 6	2. Factoriser D. D = ( + 2)^2 – ( + 2) (5 – 1) D = (+2) [ (+2) – (5 – 1)] D = (+2) (+2 – 5 + 1) D = ( + 2) ( – 4 + 3)
3. L’équation ( + 2) ( – 4 + 3) = 0 est de la forme AB=0, ce qui revient à résoudre A=0 ou B=0, soit : + 2=0 ou – 4 + 3 = 0 = – 2 ou –4 = –3 = – 2 ou = L’équation admet deux solutions : –2 et .

Exercice 3 :(/2,5)

1.Développer et réduire E. E = (7 – 3)² – 9 E = 49² – 42 + 9 – 9 E = 49² – 42

2.Factoriser E. E = (7 – 3)² – 3² de la forme a²-b² E = (7 – 3 + 3) (7 – 3 – 3) E = 7 (7 – 6)

3.l’équation 7( 7 – 6) = 0 est de la forme AB=0, ce qui revient à résoudre A=0 ou B=0, soit : 7=0 ou 7 – 6 = 0 =0 ou 7= 6 =0 ou = L’équation admet deux solutions 0 et .

Exercice 4 : (/1,5)

On calcule le PGCD de 1488 et 2418 à l’aide de l’algorithme d’Euclide : 2418 = 14881 + 930 1488 = 930 1 + 558 930 = 558 1 + 372 558 = 372 1 + 186 372 = 186 2 + 0

Donc : PGCD (2418, 1488) = 186. Pour rendre la fraction irréductible, on divise le numérateur et le dénominateur par 186 : = = fraction irréductible.

Exercice 5 :(/2,5)

Partie II : Activités géométriques (12 points)

Exercice II :(/5)

3/3