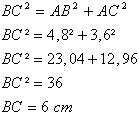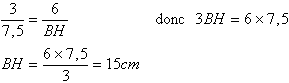EXERCICE 1:
ABC est un triangle rectangle en A tel que AB = 4,8 cm et AC = 3,6 cm
1) Faire une figure et calculer BC.
2) Calculer tan . Donner la mesure de l'angle arrondie au degré près.
3) Placer le point M du segment [AB] tel que AM=1,6 cm.
Placer le point N du segment [AC] tel que AN=1,2 cm.
4) Démontrer que les droites (MN) et (BC) sont parallèles.

EXERCICE 2:
L'unité de longueur est le centimètre.
1) Construire un triangle ABC tel que AB = 7,5 BC = 6 AC = 4,5
Démontrer que ABC est rectangle en C.
2) Le cercle de centre A et de rayon AC coupe le segment [AB] en D. La droite (AC) coupe le cercle en C et en un autre point E. Démontrer que CDE est un triangle rectangle.
3) Soit M le milieu du segment [ED]. Démontrer que les droites (AM) et (CD) sont parallèles.

4) (AM) et (CB) sont sécantes en H. En prenant BD = 3, calculer BH.

EXERCICE 1: (correction)

ABC est un triangle rectangle en A tel que AB = 4,8 cm et AC = 3,6 cm

M Î[AB] et AM = 1,6 cm. N Î[AC] tel que AN=1,2 cm.	1) Calculer BC Appliquons le théorème de Pythagore dans le triangle ABC rectangle en A	2) Calculer tan . Donner la mesure de l'angle arrondie au degré près. Dans le triangle ABC rectangle en A : Donc
4) Démontrer que les droites (MN) et (BC) sont parallèles. Dans le triangle ABC : A, M, B sont alignés A, N, C sont alignés et dans le même ordre. EXERCICE 2: (correction):			et donc D'après la réciproque du théorème de Thalès les droites (MN) et (BC) sont parallèles
			1) Dans le triangle ABC : donc D'après la réciproque du théorème de Pythagore le triangle ABC est rectangle en C. 2) Le cercle de centre A et de rayon AC coupe le segment [AB] en D. La droite (AC) coupe le cercle en C et en un autre point E. Démontrer que CDE est un triangle rectangle. [AC] est un rayon pour le cercle donc [CE] est un diamètre. D appartient au cercle. Le triangle CDE est inscrit dans le cercle de diamètre [CE] donc CDE est un triangle rectangle en D.

3) Soit M le milieu du segment [ED]. Démontrer que les droites (AM) et (CD) sont parallèles.

Dans le triangle CDE, A est le milieu de [CE] et M est le milieu de [AD].

Dans un triangle, la droite qui passe par le milieu de deux côtés est parallèle au troisième côté.

Donc (AM) et (CD) sont parallèles.